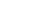悉尼科技大學(xué)微分規(guī)則主要講什么內(nèi)容?微分規(guī)則幫助我們?cè)u(píng)估某些特定函數(shù)的導(dǎo)數(shù)，而不是使用一般的微分方法。微分或求函數(shù)導(dǎo)數(shù)的過(guò)程具有重要的線(xiàn)性性質(zhì)。這一性質(zhì)使得導(dǎo)數(shù)對(duì)于使用加法和常數(shù)乘法過(guò)程從初等初等函數(shù)構(gòu)造的函數(shù)來(lái)說(shuō)更為自然。讓我們?cè)诒疚闹薪Y(jié)合實(shí)例學(xué)習(xí)微分法則。

微分規(guī)則是指導(dǎo)數(shù)的重要規(guī)則，包括：

1. 冪規(guī)則（Power Rule）
2. 和差規(guī)則（Sum and Difference Rule）
3. 乘積規(guī)則（Product Rule）
4. 商規(guī)則（Quotient Rule）
5. 鏈?zhǔn)椒▌t（Chain Rule）

讓我們逐一討論前兩個(gè)規(guī)則，并附上例子。

1.冪規(guī)則

這是導(dǎo)數(shù)中最常見(jiàn)的規(guī)則之一。如果 x 是一個(gè)變量，并被提升到冪 n，則 x 的冪的導(dǎo)數(shù)表示為：

\[ \fracg88uyea{dx}(x^n) = nx^{n-1} \]

例子：求解 \(x^5\) 的導(dǎo)數(shù)

解：根據(jù)冪規(guī)則，我們知道：

\[ \fracye28u2w{dx}(x^n) = nx^{n-1} \]

因此，\[ \fracau2wwki{dx}(x^5) = 5x^{5-1} = 5x^4 \]

2.和差規(guī)則

如果函數(shù)是兩個(gè)函數(shù)的和或差，則函數(shù)的導(dǎo)數(shù)是這些各自函數(shù)的和或差，即

\[ f(x) = u(x) \pm v(x) \]，那么

\[ f'(x) = u'(x) \pm v'(x) \]

例子1：\[ f(x) = x + x^3 \]

解：通過(guò)應(yīng)用導(dǎo)數(shù)的和規(guī)則，我們有：

\[ f'(x) = u'(x) + v'(x) \]

現(xiàn)在，對(duì)給定的函數(shù)進(jìn)行微分，我們得到：

\[ f'(x) = \frac0qs06e2{dx}(x + x^3) \]

\[ f'(x) = \fracacouqw2{dx}(x) + \fracui66ua0{dx}(x^3) \]

\[ f'(x) = 1 + 3x^2 \]

例子2：求解函數(shù) \( f(x) = 6x^2 - 4x \) 的導(dǎo)數(shù)

解：

給定函數(shù)為：\( f(x) = 6x^2 - 4x \)

這是形式為 \( f(x) = u(x) - v(x) \)

因此，通過(guò)應(yīng)用導(dǎo)數(shù)的差規(guī)則，我們得到：

\[ f'(x) = \frackyqqsim{dx}(6x^2) - \fracmeaugcq{dx}(4x) \]

\[ = 6(2x) - 4(1) \]

\[ = 12x - 4 \]

因此，\( f'(x) = 12x - 4 \)

海馬課堂專(zhuān)業(yè)課程輔導(dǎo)做出以下新改變啦：
?試聽(tīng)課全面升級(jí)，不滿(mǎn)意退50%，
?課程輔導(dǎo)產(chǎn)品升級(jí)，贈(zèng)送考前保障呦
?輔導(dǎo)不滿(mǎn)意可以隨心退！
海馬課堂，3500+嚴(yán)選碩博學(xué)霸師資，針對(duì)學(xué)生的薄弱科目和學(xué)校教學(xué)進(jìn)度，匹配背景相符的導(dǎo)師，根據(jù)學(xué)生情況進(jìn)行1V1專(zhuān)屬備課，上課時(shí)間靈活安排，中英雙語(yǔ)詳細(xì)講解課程中的考點(diǎn)、 難點(diǎn)問(wèn)題，并提供多方位的課后輔導(dǎo)，輔助學(xué)生掌握全部課程知識(shí)，補(bǔ)足短板。